这篇 paper 写的非常好，总结了近年来深度学习和有向图模型结合的部分工作。

由于有部分内容，特别是 Amortized Variational Inference 我还不是特别懂，所以暂时胡乱写写，以后有时间可能还会更新（咕咕咕）。

我主要分为三个部分进行介绍： Models, Objective 和 Inference Method.

Models

Discrete Models

考虑纯图模型的情况, 则离散隐变量 $z$ 的先验分布为：

$p(z=k; \mathbf{\mu}) = \mu_k ,$

其中 $\mu \in \Delta^{K-1} $，假设 $z$ 有 $K$ 个类别（这里 $\mathbf{\mu}$ 我加粗表示 vector 但好像看不出来什么区别，总之可能会有符号上的混乱）。

建模 given $z$ 的 input $x$ 的概率为：

$p(x | z; \mathbf{\pi_z}) = \prod_{t=1}^{T} \pi_{z,x_t} $

所以联合概率分布$p(x, z; \mathbf{\theta}) = p(z; \mathbf{\mu}) \times p(x|z; \mathbf{\pi}z)$，还可以算出input $x$ likelihood 的精确解：$p(x; \mathbf{\theta}_z) = \sum{j=1}^{k} p(x, z_j; \mathbf{\theta}) $。

事实上，这可以看作是对 instance $x_i$ 的一种聚类，聚成 $K$ 类。

神经网络参数化

原来的图模型可以用神经网络进行参数化，比如：

$p(x|z) = {\rm RNNLM}(x; \pi_z)$

同样的，我们也可以得到联合概率分布和likelihood。

后验概率

这两种方法都可以得到精确的后验分布：

$p(z|x; \theta ) = \frac{p(z)\times p(x|z)}{p(x)} = \frac{p(z)\times p(x|z)}{\sum_{k=1}^{K} p(z=k) \times p(x | z=k)}$

相比于传统模型（mixture of categoricals）神经网络参数化相对来说可以减少参数，不过与此对应，算 likelihood 的时候 RNN 就需要跑 $K$ 次。

Continuous Models

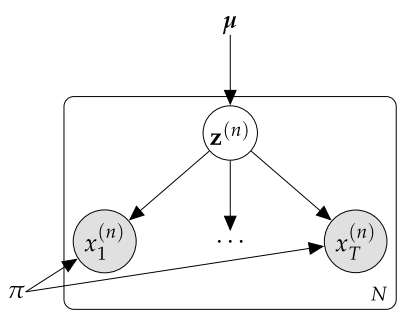
与 Discrete Models 类似，只不过 $\mathbf{z} ~\sim N(\mu, \Sigma) $ 是一个 vector 而不是代表类别的标量。所以联合概率分布为：

$p(x, \mathbf{z}; \theta) = p(\mathbf{z}; \mu) \times p(x | \mathbf{z}; \mathbf{W}) = N(\mathbf{z}; \mu, \Sigma) \times \prod_{t=1}^T {\rm softmax}(\mathbf{Wz})_{x_t}.$

神经网络参数化

类似的，我们用神经网络参数化 $p(x|\mathbf{z})$ ：

$p(x|\mathbf{z}) = {\rm CRNNLM}([\mathbf{x};\mathbf{z}])$

后验概率

显然，对于没有用神经网络参数化的模型，我们可以通过·积分算得精确后验分布，但对于神经网络参数化的模型，我们不能得到准确的后验分布。

Structured Models

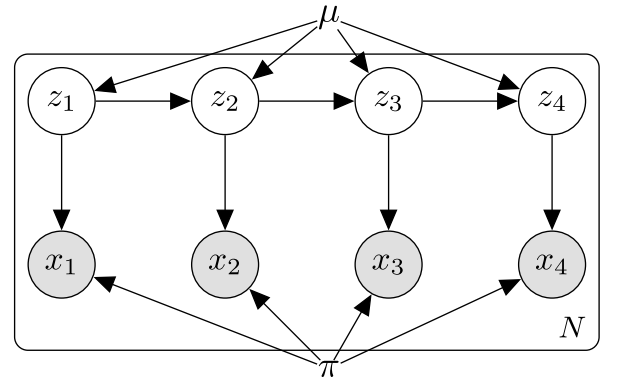
如果我们用一系列相关的离散隐变量进行建模，比如 HMM，就被称作 Structured Models。

对于普通的图模型，以不知有 $x$ 和 $z$ 之间的生成关系，还有 $z$ 之间的转移关系：

$p(x, z; \theta) = \prod_{t=1}^{T} p(z_t|z_{t-1}) \times \prod_{t=1}^{T} p(x_t|z_{t})$

神经网络参数化

我们可以用神经网络参数化 $z$ 与 $x$ 之间的生成关系和 $z$ 之间的转移关系：

$p(x_t | z_t) = {\rm softmax}({\rm MLP}(z_t))$ $p(z_t | z_{t-1}) = {\rm softmax}({\rm MLP}(z_{t-1}))$

后验概率

在某些模型中，我们可以通过动态规划算出 $p(z | x; \theta)$ ，比如 HMM 或者 PCFG，但也有不可以的，比如 Factorial HMM。

Variational Objective

Maximizing the Log Marginal Likelihood

对于可以计算 likelihood 的模型（比如上文提及的 Discrete Models），我们可以直接优化 ${\rm log}(x; \theta)$。注意，如果可以计算 likelihood，这样当于可以计算后验分布 $p(z|x)$。

梯度更新公式见paper。

Expectation Maximization (EM) Algorithm

有些时候，我们无法直接计算出 $p(x; \theta)$ 或者 $p(x,z; \theta)$，但是我们可以算出$p(z | x; \theta)$，这种时候，我们优化 likelihood 的 lower bound。

E-step 计算后验概率
通过 expected complete data likelihood 进行参数迭代优化。

具体可以看 PRML P450.

Variational Inference

Variational inference 是在 $p(z | x; \theta)$ 也无法精确计算的情况下用一个可计算的 $q(z; \lambda)$ 来估计 $p(z | x; \theta)$ 的方法。它也不能直接优化 $p(x)$，也是只能优化 $p(x)$ 的一个lower bound (evidence lower bound, ELBO)。

${\rm ELBO}(\theta, \lambda; x) = E_{q(z; \lambda)} {\rm log} \frac{p(x, z; \theta)}{q(z; \lambda)} $

具体推导可以看 paper 或者 PRML.

Inference Strategies

我们这里考虑如何优化 ELBO 。

Exact Gradient

对于目标函数 ${\rm argmax}_{\theta, \lambda} {\rm ELBO}(\theta, \lambda)$，我们对于 $\theta$ 和 $\lambda$ 求导：

$\nabla_{\theta} {\rm ELBO}(\theta, \lambda) = E_{q(z; \lambda)} \nabla_{\theta} {\rm log} \, p(x, z; \theta)$ $\nabla_{\lambda} {\rm ELBO}(\theta, \lambda) = \nabla_{\lambda} E_{q(z; \lambda)} {\rm log} \frac{p(x, z; \theta)}{q(z; \lambda)}$

事实上，对 $\lambda$ 求导依然是很困难的。

Sampling

对 $\nabla_{\lambda} {\rm ELBO}(\theta, \lambda) $ 通过化简，我们可以得到：

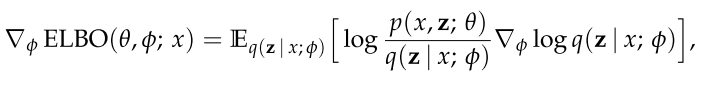
对于 VAE 我们可以通过 reparameterizable trick 计算导数。

这部分写的太简略了，建议直接看纸或者VAE的原纸，我想回宿舍装电脑了。。

Conjugacy

这是用来处理 $p(z | x; \theta)$ 是 intractable 但 $p(x, z; \theta)$ 是 conditionally conjugate 情况下的方法。

这一部分我不懂，而且是出现在 PPT 里，tutorial 里几乎没有涉及的部分，我还有很多地方不理解，先不写了。

Other Inference Methods

这里的其他方法说的是针对 VAE 之类的不能计算 $p(z | x)$ 的模型的扩展方法。

Gumbel-softmax: 是 reparameterizable trick 针对离散变量的一种扩展
Flows: 是一种让 $q$ 形式更多样，用来 tighter bound 的方法。
Importance Weighting: 也是 tighter bouond 的方法，通过对 $q$ 进行 importance sampling.

以上都是针对 explicit latent variable method 的一系列方法，针对 implicit latent variable method 比如 GAN 等模型，还有非常多可以说的。