A Transition-based constituent parsing method and this method can be used to dependency parsing,

Background

Transition-based constituent parsing

Transition-based constituent parsing takes a left-to-right scan of the input sentence, where a stack is used to maintain partially constructed phrase-structures, while the input words are stored in a buffer. Formally a state is defined as $[\sigma, i, f]$, where $\sigma$ is the stack, $i$ is the front index of the buffer, and $f$ is a boolean value showing if the parsing is finished. At each step, a transition action is applied to consume an input word or construct a new phrase-structure. Different parsing systems employ their own set of actions.

Bottom-up System

SHIFT: pop the front word from the buffer, and push it onto the stack.
REDUCE-L/R-X: pop the top constituents off the stack, combine them into a new constituent with label X, and push the new constituent onto the stack.
UNARY-X: pop the top constituent off the stack, raise it to a new constituent with label X, and push the new constituent on to the stack.
FINISH: pop the root node off the stack and ends parsing.

Top-down System

SHIFT: pop the front word from the buffer, and push it onto the stack.
NT-X: open a nonterminal with label X on the top of the stack.
REDUCE: repeatedly pop completed subtrees of terminal symbols from the stack until an open nonterminal is encountered, and then this open NT is popped and used as the label of a new constituent that the popped subtrees as its children. This new completed constituent is pushed onto the stack as a single composite item.

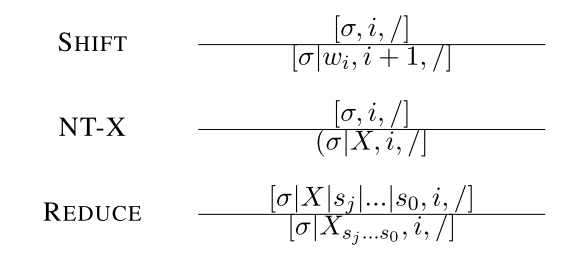
Stack-LSTM

Compare with conventional LSTM, stack-LSTM augment the LSTM with a “stack pointer”. Like the conventional LSTM, new inputs always added in the right-most position, but in stack LSTMs, the current location of the stack pointer determines which cell in the LSTM provides $c_{t-1}$ and $h_{t-1}$ when computing the new memory cell contents.

Push: adding elements to the ends of the sequence.
Pop: moves the stack pointer to the previous elements.

With this two operations, the LSTM can be understood as a stack implemented so that contents are never overwritten, that is, push always adds a new entry at the end of the list that contains a back-pointer to the previous top, and pop only updates the stack pointer.

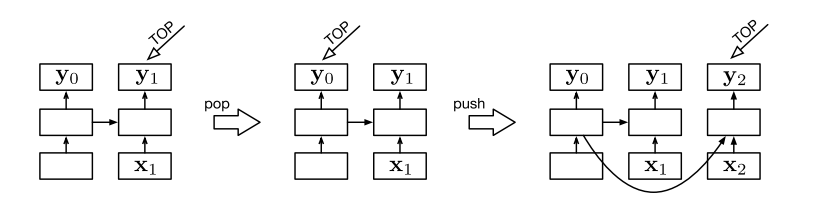
The picture above is a case of how stack LSTM work. The left means the stack LSTM with a single element. After a pop operation it turns to the middle, and then the result of applying a push operation is right,The boxes in the lowest rows represent stack contents, which are the inputs to the LSTM, the upper rows are the outputs of the LSTM, and the middle rows are the memory cells (the $c_t$’s and $h_t$’s) and gates. Arrows represent function applications (usually affine transformations followed by a nonlinearity).

Model

In-order System

Syntactic trees of the sentence The little boy likes red tomatoes..

Post-order System

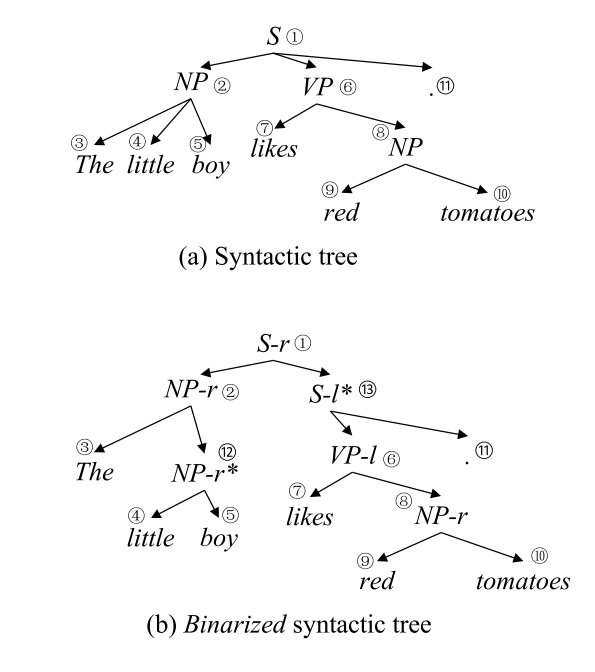
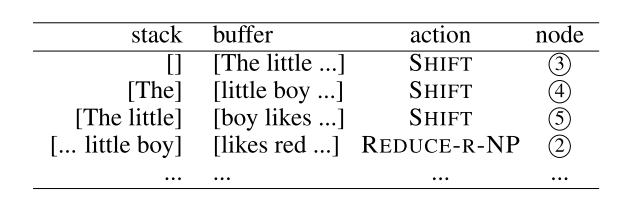
The process of bottom-up parsing can be regarded as post-order traversal over a constituent tree. For example, given the sentence in image above, a bottom-up shift reduce parser takes the action sequence in table below.

The full order of recognition for the tree nodes is $3\rightarrow4\rightarrow5\rightarrow2\rightarrow7\rightarrow9\rightarrow10\rightarrow8\rightarrow6\rightarrow11\rightarrow1$.

Pre-order System

The process of bottom-up parsing can be regarded as pre-order traversal over a constituent tree. For example, given the sentence in image above, a top-down shift reduce parser takes the action sequence in table below.

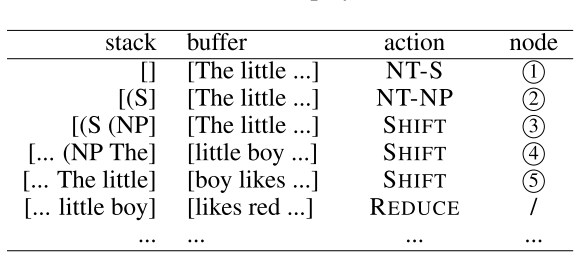
The full order of recognition for the tree nodes is $1\rightarrow2\rightarrow3\rightarrow4\rightarrow5\rightarrow6\rightarrow7\rightarrow8\rightarrow9\rightarrow10\rightarrow11$.

In-order System

Combine with the bottom-up and top-down system, the in-order system like that:

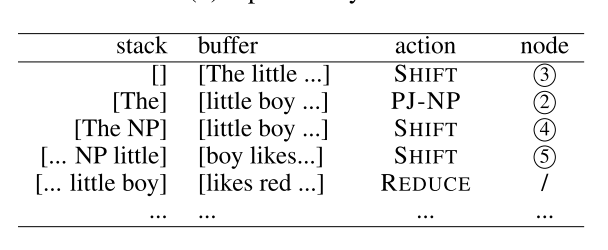
The full order of recognition for the tree nodes is $3\rightarrow2\rightarrow4\rightarrow5\rightarrow1\rightarrow7\rightarrow6\rightarrow9\rightarrow8\rightarrow10\rightarrow11$.

The set of transition actions are defined as:

SHIFT: pop the front word from the buffer, and push it onto the stack.
PJ-X: project a nonterminal with label X on the top of the stack.
REDUCE: repeatedly pop completed subtrees or terminal symbols from the stack until an projected nonterminal is popped and used as the label of a new constituent, and furthermore, one more item on the top of stack is popped as the leftmost child of the new constituent and the popped as the leftmost child of the new constituent and the popped subtrees as its rest children. This new completed constituent is pushed onto the stack as a single composite item.
FINISH: pop the root node off the stack and ends parsing.

Neural Parsing Model

Word representation

This paper combing three different part of word embedding to represent the word:

pretrained word embedding, ${\overline{e}}_{w_i}$
randomly initialized embeddings, $e_{w_i}$
randomly initialized part-of-speech embedding, $e_{p_i}$

$x_i =f(W_{input}[e_{p_i}; \overline{e}_{w_i}; e_{w_i} + b_{input} ]) $

Stack representation

This paper employs a bidirectional LSTM as the composition function to represent constituents on stack.

Greedy action classification

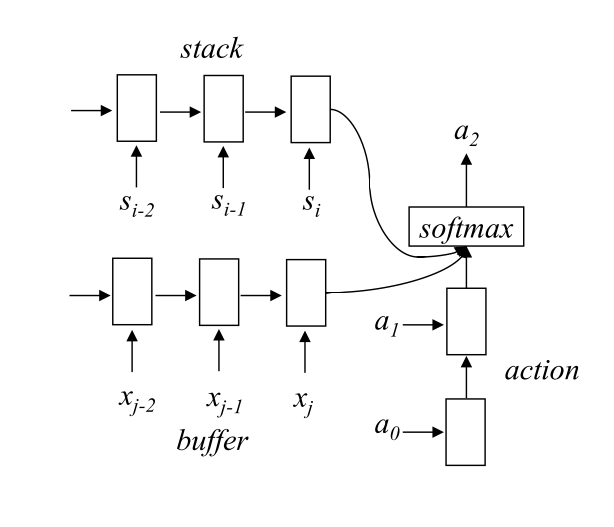
Given a sentence $w0, w_1, …, w{n-1}$, where $w_i$ is the $i$th word, and $n$ is the length of the sentence, our parser makes local action classification decisions incrementally. For the $k$th parsing state like $[s_j, …, s_1, s_0, i, false]$, the probability distribution of the current action $p$ is:

$p = SOFTMAX(W[h_{stk} ; h_{buf}; h_{ah} + b])$

where $W$ and $b$ are model parameters, the representation of stack information $h_{stk}$ is

$h_{stk} = stack-LSTM[s_0, s_1, ..., s_j]$

the representation of buffer information $h_{buf}$ is

$h_{buf} = stack-LSTM[x_i, x_{i+1}, ..., x_n]$

$x$ is the word representation, and the representation of action history $h_{ah}$ is

$h_{ah} = LSTM[e_{act_{k-1}}, e_{act_{k-1}}, ..., e_{act_0}]$

where $e{act{k-1}}$ is the representation of action in $k-1$th parsing state.

Training minimize the cross-entropy loss objective with an $l_2$ regularization term:

$L(\theta) = -\sum_{i}\sum_{j}log p_{a_{ij}} + \frac{\lambda}{2}||\theta||^{2}$

Experiment

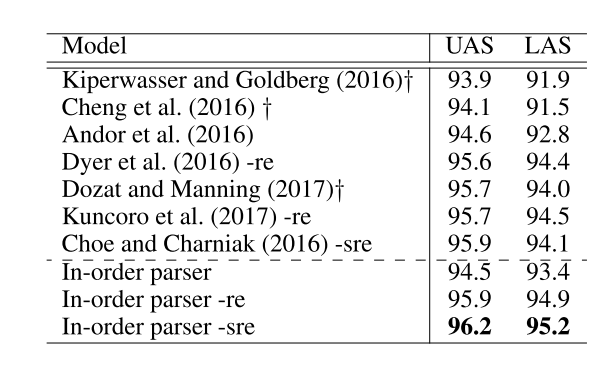
Dependency parsing on WSJ section 23. “-re” means fully-supervised reranking and “-sre” means semi-supervised reranking.

Comment

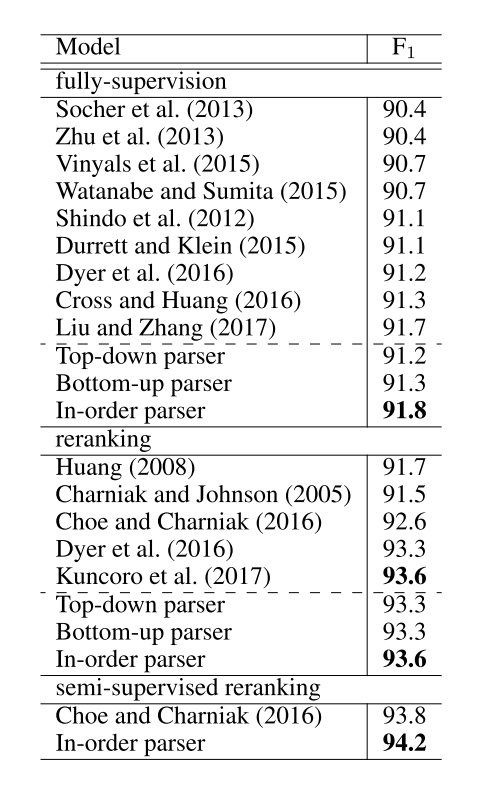
This paper proposed a constituent parsing system based on the in-order traversal over syntactic trees, aiming to find a compromise between bottom-up constituent information and top-down lookahead information. The parser archives 91.8 F1 score in WSJ section 23.

The idea of this paper is very straightforward but clever, it just combine two previous work and get a state-of-art performance. Based on stack-LSTM, it can be implement very easily by tensorflow or pytouch. Beside that, It’a very basic idea so that the idea can be implement to constituent parsing and dependency parsing, it can also be used to train a semi-supervised model.