Brief
This work focus on commonsense knowledge. As described in this paper, they propose a new commonsense approach to address two problem:
- How to mine and represent different kinds of implicit knowledge that commonsense machine comprehension needs
- How to reason with various kinds of commonsense knowledge.
Background
RocStories Dataset
Given 4 sentence, select the right result.
| Premise Document | Premise Document | Wrong Hypothesis |
|---|---|---|
| Ron started his new job as a landscaper today. He loves the outdoors and has always enjoyed working in it. His boss tells him to re-sod the front yard of the mayor’s home. Ron is ecstatic, but does a thorough job and finishes super early |
His boss commends him for a job well done. | Ron is immediately fired for insubordination. |
| One day, my sister came over to the house to show us her puppy. She told us that she had just gotten the puppy across the street. My sons begged me to get them one. I told them that if they would care for it, they could have it. |
My son said they would, so we got a dog. | We then grabbed a small kitten. |
Commonsense Knowledge Acquisition for Machine Comprehension
Three types of commonly used commonsense knowledge:
- Event narrative knowledge, which captures temporal and causal relations betweens events;
- Entity semantic knowledge, which captures semantic relations between entities;
- Sentiment coherent knowledge, which captures sentimental coherence between elements.
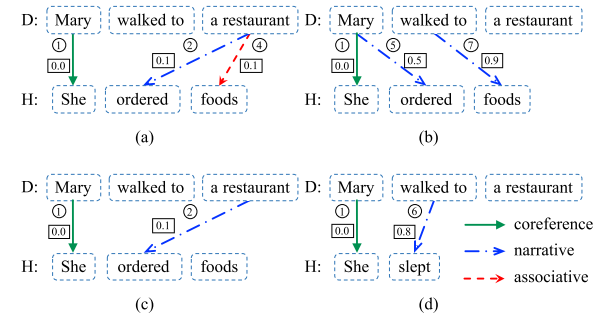
Samples of these knowledge:
| Antecedent | Consequent | Relation | Cost | |
|---|---|---|---|---|
| ① | Mary | she | co-reference | 0.0 |
| ② | restaurant | order | narrative | 0.1 |
| ③ | restaurant | food | associative | 0.1 |
| ④ | restaurant | food | narrative | 0.3 |
| ⑤ | Mary | order | narrative | 0.5 |
| ⑥ | walk | sleep | narrative | 0.8 |
| ⑦ | walk | food | narrative | 0.9 |
Format to represent knowledge
It means element $Y$ can be inferred form element $X$ under relation $f$, with an inference cost $s$. An element can stand for either event, entity or sentiment.
Mining Event Narrative Knowledge
Instance: We can infer “X ordered some foods” form “X walked to a restaurant” using narrative knowledge.
This paper proposes two models to encode this knowledge using inference rules.
First is based on ordered PMI. Given two element $e_1$ and $e_2$, this model calculates the cost of inference rule $e_1 \stackrel{narrative}{\longrightarrow} e_2$ as:
Here $C(e_1, e_2)$ is the order sensitive count that element $e_1$ occurs before element $e_2$ in different sentences of the same document.
Second is a variant of the skip-gram model. The model aims to find a element representations that can accurately predict relevant elements in sentences afterwards. Given $n$ asymmetric pairs of elements $(e1^1, e_2^1)$, $(e_1^2, e_2^2)$, … ,$(e_1^n, e_2^n)$ identified from training data, the objective of this model is to maximize the average log probability $\frac{1}{n} \sum{i=1}^{n}log{P(e_2^i|e_1^i)}$ and the prob $P(e_2| e_1)$ is defined using the softmax function:
where $\mathbf{v}_e$and $\mathbf{v’}_e$ are “antecedent” and “consequent” vector representation of element $e$. And they use the nagative inner product as the cost of inference rule.
Mining Entity Semantic Knowledge
Instance: if a premise document contains “Starbucks”, then “coffeehouse” and “lat- te” will be reasonable entities in hypothesis since “Starbucks” is a possible coreference of “coffee- house” and it is semantically related to “latte”.
- Co-reference relation,which indicates that two elements refer to the same entity in environment. Actually, an entity is often referred using its hypernyms. So using Wordnet information build inference rule $X \stackrel{coref}{\longrightarrow} Y$. Cost is 0 if these two elements are lemmas in the same Wordnet synset, or with hypernyms relation in Wordnet. Otherwise, the cost is 1.
- Associative relation, which captures the semantic relatedness between two entities.“starbucks” → “latte”, “restaurant” → “food”, etc. And represent the semantic distance $dist(e_1, e_2)$, detail see paper.
Mining Sentiment Coherent Knowledge
i.e., a reasonable hypothesis should be sentimen- tal coherent with its premise document.
First setting a word is positivity, negativity or objectivity. Then setting inference rules’ cost by element has the same polarity or not.
Metric Learning to Calibrate Cost Measurement
So far, we have many inference rules under different relations. we need a metric to calibrate inference rule cost. So using the metric learning, this paper use a non-linear layer to the original cost $s_r$ of inference rule $r$ under relation $f$:
Calibration parameters will be trained along with other parameters in model.
Dealing with Negation
The existence of negation is detected using dependency relations(dependency parse?). And set the cost of negation inference rules is $1-s$
Machine Comprehension via Commonsense Reasoning
There is the model this paper used.
Three part: 1) how to infer from a premise document to a hypothesis using inference rules. 2)how to choose inference rules for a specific reasoning context. 3) how to measure the reasoning distance from a premise document to a hypothesis by summarizing the costs of all possible inferences.
Premise document $D = { d_1, d_2, …, d_m}$, m elements.
Hypothesis $H = {h_1, H_2, …, H_n }$, n elements
Valid inference set $R$ from $D$ to $H$, all element in $H$ can be inferred from one element in $D$ using one and only one rule in $R$. So all elements in $H$ should be covered by consequents of inference rules in $R$, as well as all antecedents of inference rules in $R$ should come from $D$. So the size of $R$ and the size of $H$ are equal. $R = { r_1, r_2, … r_n}$
Inference from Premise Document to Hypothesis
The cost of an inference $R$ as the cost sum of all inference rules in $R$.
Modeling Inference Probability using Attention Mechanism
The “cost” measures the “correctness” of an inference rule. A rule with low cost is more likely to be “reasonable”, and a rule with high cost is more likely to be a contradiction with commonsense. On the other hand, the “possibility” should measure how likely a rule will be applied in a given context, which does not depend on the “cost” but on the nature of the rule and the given context.
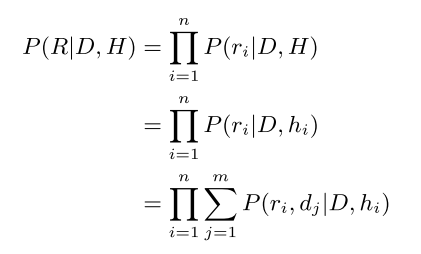
and the $P$ in the last line is the defined as:
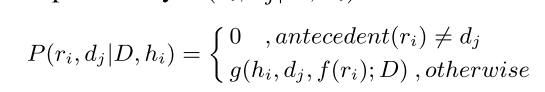
$g$ is :
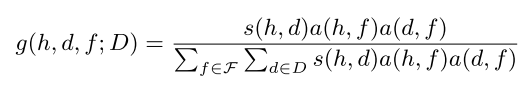
Reasoning Distance Between Premise Document and Hypothesis
Given a premise document, this section shows how to measure whether a hypothesis is coherent using above inference model. $L(D →H)$ as the expected cost sum of all valid inferences:
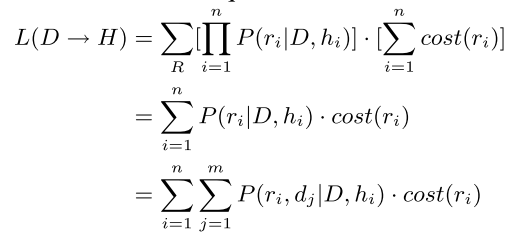
Model Learning
Define the posterior probability :
learning the log likelihood of choosing the right hypothesis $H^+$ for $D$:
Experiments
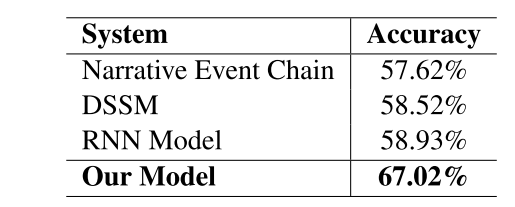
Compare with baseline:
Compare with only one source:

Compare with drop out one source:
