Style Transfer from Non-Parallel Text by Cross-Alignment

This work comes from Tommi Jaakkola. In vision, style transfer is a mature work. But in language, there not so many attention paid on this. Many work learning style transfer from parallel data, but actually there is not so many parallel data. So this paper is focus on learning a style transfer model from non-parallel text.

Formulation

First, this paper assumes a sentence generate by the following process:

1. A latent style variable $\textbf{y}$ is generated from some distribution $p(\textbf{y})$;
2. A latent content variable $\textbf{z}$ is generated from some distribution $p(\textbf{z})$;
3. A data point $\textbf{x}$ is generated from conditional distribution $p(\textbf{x|y, z})$.

So this work focus on that: we know dataset $p(\textbf{x}_1|\textbf{y}_1)$ and $p(\textbf{x}_2|\textbf{y}_2)$ where $\textbf{y}_1$ and $\textbf{y}_2$ is unknown. And we want to learn the style transfer functions between them, namely $p(\textbf{x}_1|\textbf{x}_2 ; \textbf{y}_1, \textbf{y}_2)$ and $p(\textbf{x}_2|\textbf{x}_1 ; \textbf{y}_1, \textbf{y}_2)$.

Then the paper proof that: If we see style $\textbf{y} = (\textbf{A}, \textbf{b})$ as an affine transformation, i.e. $\textbf{x} = \textbf{Ay} + \textbf{b} + \epsilon$ where $\epsilon$ is noise, the distribution $\textbf{z}$ cannot be simple, it should be a complex distribution like Gaussian Distribution with more than two components. Only that can recover the transfer give their respective marginals.

Last, example word substitution suggest that $\textbf{z}$ as the latent content variable should carry most complexity of data $\textbf{x}$. while $\textbf{y}$ as the latent style variable should have relatively simple effects.

Method

Through the way to calculate $p(\textbf{x}_1| \textbf{x}_2; \textbf{y}_1, \textbf{y}_2)$:

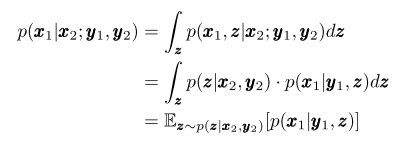
So we can learning with a autoencoder.

If use a variational auto encoder, we can get the reconstruction loss is :

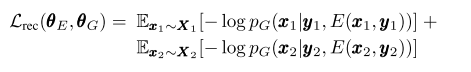
There $E : X \times Y \rightarrow Z$ be a deterministic encoder that infers the mas of content variable $\textbf{z}$ for a given sentence $\textbf{x}$ from a given style style $\textbf{y}$. let $G : Y \times Z \rightarrow X$ be a probabilistic generator that generates a sentence $\textbf{x}$ from a given style $\textbf{y}$ and centent $\textbf{z}$.

Aligned auto-encoder

This method is VAE add a constrain : both $\textbf{x}_1$ and $\textbf{x}_2$ are generated using the same latent distribution $p(\textbf{z})$. So the objective function add a Lagrangian relaxation term:

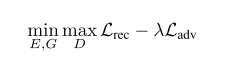
where :

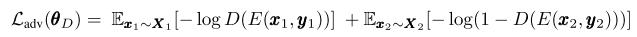
Cross-aligned auto-encoder

Under the generative assumption, we can get $p(x_2 | y_2 )$ as follow:

$$p(x_2|y_2) = \int_{ x_1 } { x_1 p(x_2|x_1;y_1,y_2) p(x_1|y_1) } dx_1 ,$$

thus $x_2$ (sampled from the left-hand side) should exhibit the same distribution as transferred $x_1$ (sampled from the right-hand side), and vice versa. So add a similar constrain.

Learning

1. Instead of training over the discrete sampless generated by $G$, it use softmax distribution.
2. use Professor-Forcing.(Clear I’m not familiar with this method, I will write this part after I know this algorithm)